袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用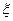
表示取出的3个小球上的最大数字．
（Ⅰ）取出的3个小球上的数字互不相同的概率；
（Ⅱ）随机变量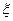的概率分布和数学期望；
（Ⅲ）计分介于20分到40分之间的概率．
相关试题
的最小正周期T；
，b，c分别为△ABC内角A，B，C的对边，A为锐角，
上的最大值，求A，b和△ABC的面积.
中，角
、
、
所对应的边分别为
、
、
，且满足
．
，求
的值．
是坐标原点，且
，
.
，求
的值；
，求
的值域．
的值；
的值
，
,
，
，
，
为正实数.
，求
的值;
，求
时，若
，试确定
与
的关系式.推荐套卷
袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用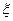表示取出的3个小球上的最大数字．
（Ⅰ）取出的3个小球上的数字互不相同的概率；
（Ⅱ）随机变量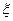的概率分布和数学期望；
（Ⅲ）计分介于20分到40分之间的概率．
粤公网安备 44130202000953号