（本小题满分8分）如图，等腰直角三角
形ABC，AB=
，点E是
斜边AB上的动点，过E点做矩形EFCG，设矩形EFCG面积为S，矩形一边EF长为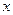
，
（1）将S表示为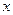的函数，并指出函数的定义域；
（2）当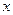为何值时，矩形面积最大。（写出过程）
相关知识点
推荐套卷
（本小题满分8分）如图，等腰直角三角形ABC，AB=，点E是斜边AB上的动点，过E点做矩形EFCG，设矩形EFCG面积为S，矩形一边EF长为，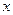
（1）将S表示为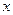的函数，并指出函数的定义域；
（2）当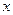为何值时，矩形面积最大。（写出过程）
粤公网安备 44130202000953号