(14分)已知函数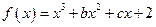 .
.
(1)若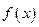 在
在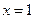 时,有极值
时,有极值 ,求
,求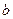 、
、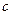 的值.
的值.
(2)当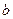 为非零实数时,
为非零实数时,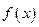 是否存在与直线
是否存在与直线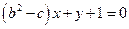 平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.
平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.
(3)设函数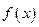 的导函数为
的导函数为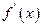 ,记函数
,记函数 的最大值为M,求证
的最大值为M,求证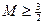 .
.
推荐套卷
(14分)已知函数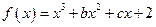 .
.
(1)若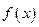 在
在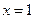 时,有极值
时,有极值 ,求
,求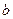 、
、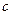 的值.
的值.
(2)当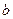 为非零实数时,
为非零实数时,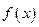 是否存在与直线
是否存在与直线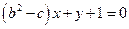 平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.
平行的切线,如果存在,求出切线的方程,如果不存在,说明理由.
(3)设函数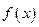 的导函数为
的导函数为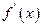 ,记函数
,记函数 的最大值为M,求证
的最大值为M,求证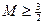 .
.