(本小题满分13分)已知 、
、 ,椭圆C的方程为
,椭圆C的方程为 ,
, 、
、 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设 为椭圆C上一点,存在以
为椭圆C上一点,存在以 为圆心的
为圆心的 与
与 外切、与
外切、与 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作斜率为
作斜率为 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与 轴相交于点D,若
轴相交于点D,若 求
求 的值;
的值;
(Ⅲ)已知真命题:“如果点T( )在椭圆
)在椭圆 上,那么过点T
上,那么过点T
的椭圆的切线方程为 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
推荐套卷
 的前
的前 项和为
项和为 ,且
,且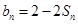 ;数列
;数列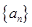 为等差数列,且
为等差数列,且 ,
, .
. ,
,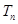 为数列
为数列 的前
的前
 ,求
,求 ;
;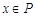 是
是 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.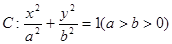 上的任意一点到它的两个焦点
上的任意一点到它的两个焦点 ,
, 
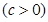 的距离之和为
的距离之和为 ,且其焦距为
,且其焦距为 .
.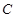 的方程;
的方程;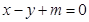 与椭圆
与椭圆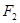 .若存在,求出
.若存在,求出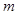 的值;不存在,说明理由.
的值;不存在,说明理由.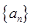 的前
的前 项和为
项和为 .已知
.已知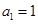 ,
,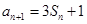 ,
,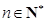 .
.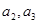 的值,并求数列
的值,并求数列 为数列
为数列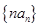 的前
的前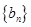 满足
满足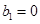 ,
, ,求数列
,求数列 时,求函数f(x)的极小值.
时,求函数f(x)的极小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号