在直角坐标系xOy中，椭圆C1：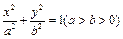
的左、右焦点分别为F1、F2，其中右焦点F2也是拋物线C2：y2 = 4x的焦点，点M为C1与C2在第一象限的交点，且|MF2| = 
．
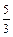（1）求椭圆C1的方程；
（2）设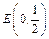
，是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点，且|AE| = |BE|？若存在，求k的取值范围；若不存在，请说明理由．
相关试题
γ=a
求证：a⊥α
平面ABC，PA=PB=PC，∠APB=∠APC=60°，∠BPC=90°求证：平面ABC⊥平面PBC
推荐套卷
在直角坐标系xOy中，椭圆C1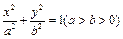：的左、右焦点分别为F1、F2，其中右焦点F2也是拋物线C2：y2 = 4x的焦点，点M为C1与C2在第一象限的交点，且|MF2| = ．
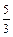（1）求椭圆C1的方程；
（2）设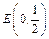，是否存在斜率为k (k≠0)的直线l与椭圆C1交于A、B两点，且|AE| = |BE|？若存在，求k的取值范围；若不存在，请说明理由．
粤公网安备 44130202000953号