已知半椭圆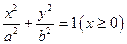 与半椭圆
与半椭圆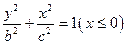 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中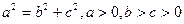 ,
,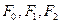 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(1) 若三角形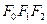 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
(2)若“果圆”方程为: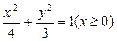 ,
,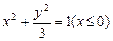 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
(3) 若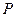 是“果圆”上任意一点,求
是“果圆”上任意一点,求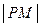 取得最小值时点
取得最小值时点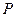 的横坐标.
的横坐标.
推荐套卷
已知半椭圆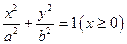 与半椭圆
与半椭圆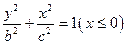 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中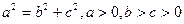 ,
,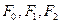 是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
是对应的焦点。A1,A2和B1,B2是“果圆”与x,y轴的交点,M是线段A1A2的中点.
(1) 若三角形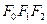 是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
是底边F1F2长为6,腰长为5的等腰三角形,求“果圆”的方程;
(2)若“果圆”方程为: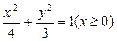 ,
,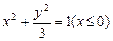 过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
过F0的直线l交“果圆”于y轴右边的Q,N点,求△OQN的面积S△OQN的取值范围
(3) 若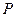 是“果圆”上任意一点,求
是“果圆”上任意一点,求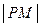 取得最小值时点
取得最小值时点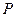 的横坐标.
的横坐标.