在各项均为正数的数列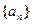 中,前
中,前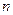 项和
项和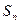 满足
满足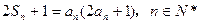 。
。
(1)证明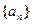 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前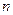 项和的公式;
项和的公式;
(2)在平面直角坐标系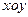 面上,设点
面上,设点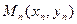 满足
满足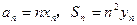 ,且点
,且点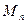 在直线
在直线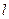 上,
上,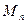 中最高点为
中最高点为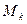 ,若称直线
,若称直线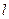 与
与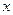 轴、直线
轴、直线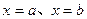 所围成的图形的面积为直线
所围成的图形的面积为直线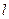 在区间
在区间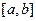 上的面积,试求直线
上的面积,试求直线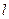 在区间
在区间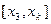 上的面积;
上的面积;
(3)若存在圆心在直线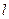 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列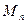 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.
推荐套卷
在各项均为正数的数列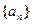 中,前
中,前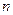 项和
项和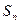 满足
满足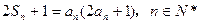 。
。
(1)证明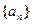 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前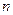 项和的公式;
项和的公式;
(2)在平面直角坐标系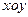 面上,设点
面上,设点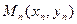 满足
满足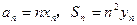 ,且点
,且点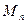 在直线
在直线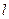 上,
上,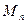 中最高点为
中最高点为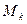 ,若称直线
,若称直线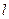 与
与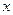 轴、直线
轴、直线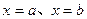 所围成的图形的面积为直线
所围成的图形的面积为直线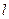 在区间
在区间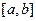 上的面积,试求直线
上的面积,试求直线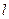 在区间
在区间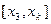 上的面积;
上的面积;
(3)若存在圆心在直线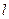 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列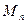 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.