（本小题满分共12分）已知函数
，
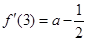
（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值；
（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m﹣x）=k对于定义域内的任意x都成立；
相关试题
;
.
,b=9.求：
.
≤a≤推荐套卷
（本小题满分共12分）已知函数，
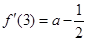
（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值；
（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m﹣x）=k对于定义域内的任意x都成立；
粤公网安备 44130202000953号