（本小题满分12分）如图几何体中，四边形ABCD为矩形，AB=3BC=6，EF =4，BF=CF=AE=DE=2， EF∥AB，G为FC的中点，M为线段CD上的一点，且CM =2．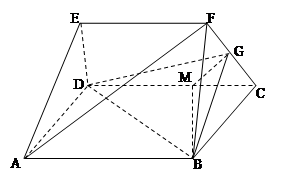
（Ⅰ）证明：平面BGM⊥平面BFC；
（Ⅱ）求三棱锥F－BMC的体积V．
相关试题
的三个顶点坐标为分别为：
试判断
，求证：直线
在同一个平面内。
满足
，
满足
，
。．
=1且
。设m
N
，m
n
+
）
（m-n+1）
是方程
的两个不等实根，函数
的定义域为
。
；
，若
。
，点P到直线BC的距离是该点到直线AB，AC距离的等比中项。
的内心（设为D），且与P点的轨迹恰好有3个公共点，求L的斜率k的取值范围。相关知识点
推荐套卷
（本小题满分12分）如图几何体中，四边形ABCD为矩形，AB=3BC=6，EF =4，BF=CF=AE=DE=2， EF∥AB，G为FC的中点，M为线段CD上的一点，且CM =2．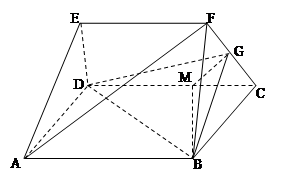
（Ⅰ）证明：平面BGM⊥平面BFC；
（Ⅱ）求三棱锥F－BMC的体积V．
粤公网安备 44130202000953号