如图,在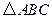 中,
中,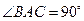 ,
,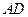 是
是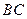 边上的高,
边上的高,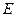 是
是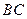 边上的一个动点(不与
边上的一个动点(不与 重合),
重合), ,
,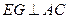 ,垂足分别为
,垂足分别为 .
.
(1)求证: ;
;
(2) 与
与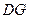 是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当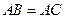 时,
时,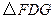 为等腰直角三角形吗?并说明理由.
为等腰直角三角形吗?并说明理由.
相关知识点
推荐套卷
如图,在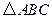 中,
中,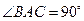 ,
,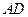 是
是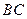 边上的高,
边上的高,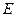 是
是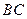 边上的一个动点(不与
边上的一个动点(不与 重合),
重合), ,
,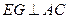 ,垂足分别为
,垂足分别为 .
.
(1)求证: ;
;
(2) 与
与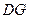 是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
是否垂直?若垂直,请给出证明;若不垂直,请说明理由;
(3)当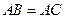 时,
时,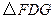 为等腰直角三角形吗?并说明理由.
为等腰直角三角形吗?并说明理由.