田忌和齐王赛马是历史上有名的故事，设齐王的三匹马分别为A、B、C，田忌的三匹马分别为a、b、c；三匹马各比赛一次，胜两场者为获胜。若这六匹马比赛优、劣程度可以用以下不等式表示：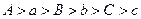
(1)正常情况下，求田忌获胜的概率
(2)为了得到更大的获胜机会，田忌预先派出探子到齐王处打探实情，得知齐王第一场必出上等马A，于是田忌采用了最恰当的应对策略，求这时田忌获胜的概率
相关试题
的极值．
＋
）n的展开式中，前三项的系数成等差数列，求展开式中的有理项．
，函数
的定义域为
且
，
当
时有
；
的值；
的单调区间．
.
；
,且最大边的边长为
，求最小边的边长.推荐套卷
田忌和齐王赛马是历史上有名的故事，设齐王的三匹马分别为A、B、C，田忌的三匹马分别为a、b、c；三匹马各比赛一次，胜两场者为获胜。若这六匹马比赛优、劣程度可以用以下不等式表示：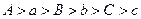
(1)正常情况下，求田忌获胜的概率
(2)为了得到更大的获胜机会，田忌预先派出探子到齐王处打探实情，得知齐王第一场必出上等马A，于是田忌采用了最恰当的应对策略，求这时田忌获胜的概率
粤公网安备 44130202000953号