(本小题满分14分)已知动圆过定点F(2,0),且与直线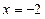 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线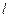 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为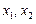 .①求证:
.①求证: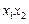 为定值;②试用
为定值;②试用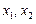 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。
相关知识点
推荐套卷
(本小题满分14分)已知动圆过定点F(2,0),且与直线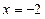 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线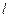 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为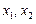 .①求证:
.①求证: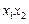 为定值;②试用
为定值;②试用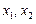 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。