已知集合 ,
,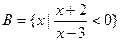
(1)求A B,A
B,A B;
B;
(2)在区间(-4,4)上任取一个实数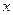 ,求“
,求“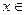 A
A B”的概率;
B”的概率;
(3)设( ,
,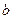 )为有序实数对,其中
)为有序实数对,其中 是从集合A中任意的一个整数,
是从集合A中任意的一个整数,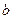 是从集合B中任取一个整数,求“
是从集合B中任取一个整数,求“ A
A B”的概率。
B”的概率。
推荐套卷
已知集合 ,
,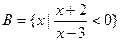
(1)求A B,A
B,A B;
B;
(2)在区间(-4,4)上任取一个实数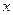 ,求“
,求“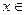 A
A B”的概率;
B”的概率;
(3)设( ,
,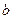 )为有序实数对,其中
)为有序实数对,其中 是从集合A中任意的一个整数,
是从集合A中任意的一个整数,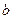 是从集合B中任取一个整数,求“
是从集合B中任取一个整数,求“ A
A B”的概率。
B”的概率。