某家具城进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为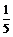
，若中奖，则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌，得到3张奖券.
（I）求家具城恰好返还该顾客现金200元的概率；
（II）（文科）求家具城至少返还该顾客现金200元的概率．
（理科）设该顾客有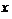
张奖券中奖，求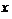的分布列，并求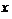的数学
期望E．
相关试题
，并且平行于极轴的直线l的极坐标方程.
=
化为直角坐标方程，并说明该方程表示什么曲线.
1=4及对应的一个特征向量e1=
，并有特征值
.
，求特征值及特征向量.
，其中a∈R，若点P（1，1）在矩阵A的变换下得到点P′（0，-3）.（1）求实数a的值；相关知识点
推荐套卷
某家具城进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为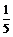，若中奖，则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌，得到3张奖券.
（I）求家具城恰好返还该顾客现金200元的概率；
（II）（文科）求家具城至少返还该顾客现金200元的概率．
（理科）设该顾客有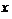张奖券中奖，求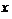的分布列，并求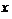的数学
期望E．
粤公网安备 44130202000953号