有三张大小形状质量完全相同的卡片,三张卡片上分别写有0,1,2三个数字,现从中任抽一张,其上面的数字记为x,然后放回,再抽一张,其上面的数字记为y,记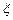 =xy,求:(1)
=xy,求:(1)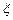 的分布列;(2)
的分布列;(2)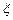 的期望.
的期望.
相关知识点
推荐套卷
有三张大小形状质量完全相同的卡片,三张卡片上分别写有0,1,2三个数字,现从中任抽一张,其上面的数字记为x,然后放回,再抽一张,其上面的数字记为y,记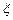 =xy,求:(1)
=xy,求:(1)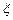 的分布列;(2)
的分布列;(2)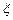 的期望.
的期望.