如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且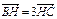 .
.
(1)若 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段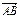 的比为
的比为 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤ ≤
≤ 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.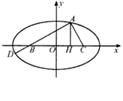
推荐套卷
如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且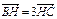 .
.
(1)若 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段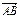 的比为
的比为 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤ ≤
≤ 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.