如图所示，O是线段AB的中点，|AB|＝2c，以点A为圆心，2a为半径作一圆，其中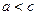
。
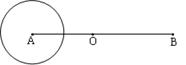
（1）若圆A外的动点P到B的距离等于它到圆周的最短距离，建立适当坐标系，求动点P的轨迹方程，并说明轨迹是何种曲线；
（2）经过点O的直线l与直线AB成60°角，当c＝2，a＝1时，动点P的轨迹记为E，设过点B的直线m交曲线E于M、N两点，且点M在直线AB的上方，求点M到直线l的距离d的取值范围。
相关试题
，若函数
图象上任意一点
关于原点的对称点
的轨迹恰好是函数
的图象
的解析式；
时，总有
成立，求实数
的取值范围．
时，求函数
的极值；
时，讨论函数
|≤ 2；命题
．若
是
的必要而不充分条件，求实数
的取值范围．
满足
．
的值；
成立的
的取值范围.
上绘制的一列抛物线和一列直线，在焦点为
的抛物线列
中，
是首项和公比都为
的等比数列，过
与
相交于
和
（
轴的上方，
的斜率是定值；
、
、
、
的面积为
，证明：数列
是等比数列，并求所有这些三角形的面积的和.
推荐套卷
如图所示，O是线段AB的中点，|AB|＝2c，以点A为圆心，2a为半径作一圆，其中。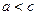
（1）若圆A外的动点P到B的距离等于它到圆周的最短距离，建立适当坐标系，求动点P的轨迹方程，并说明轨迹是何种曲线；
（2）经过点O的直线l与直线AB成60°角，当c＝2，a＝1时，动点P的轨迹记为E，设过点B的直线m交曲线E于M、N两点，且点M在直线AB的上方，求点M到直线l的距离d的取值范围。
粤公网安备 44130202000953号