已知点C为圆
的圆心，点A（1，0），P是圆上的动点，点Q在圆的半径CP上，且
（Ⅰ）当点P在圆上运动时，求点Q的轨迹方程；
（Ⅱ）若直线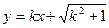
与（Ⅰ）中所求点Q的轨迹交于不同两点F，H，O是坐标原点，且
，求△FOH的面积的取值范围。
相关试题
对任意的实数
,都有
，且当
时，
;
上是单调递减的函数;
解不等式
. 
）求
的定义域、值域;
函数
在
上单调递减;
曲线
与
轴交于不同的两点．如果
且
为假命题，
,复数
,当实数
取什么值时,复数
是（1）实数;（2）纯虚数;（3）复平面内第一、三象限角平分线上的点对应的复数.
已知集合
;
,已知集合
,若
，求实数
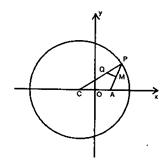
的取值范围.推荐套卷
已知点C为圆的圆心，点A（1，0），P是圆上的动点，点Q在圆的半径CP上，且
（Ⅰ）当点P在圆上运动时，求点Q的轨迹方程；
（Ⅱ）若直线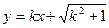与（Ⅰ）中所求点Q的轨迹交于不同两点F，H，O是坐标原点，且，求△FOH的面积的取值范围。
粤公网安备 44130202000953号