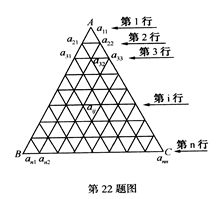
.如图，把正三角形ABC分成有限个全等的小正三角形，且在每个小三角形的顶点上都放置一个非零实数，使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行，…，BC为第n行，记点A上的数为a
，…第i行中第j个数为a
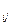（1≤j≤i）.若a
=
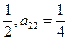
（1）求a
（2）试归纳出第n行中第m个数a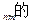
表达式（用含n,m的式子表示，不必证明）；
（3）记S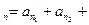
…+a
，证明：n≤
+
+…+
≤
相关试题
＝4＋2i，求复数z．
，
,
和
；
，
”的部分用阴影涂黑；
和
.
，
．
，试求函数
（
）的最小值；
，不等式
成立，试求
的取值范围．
．
，求曲线
在点
处的切线方程；
求函数
的单调区间．
，则
推荐套卷
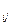.如图，把正三角形ABC分成有限个全等的小正三角形，且在每个小三角形的顶点上都放置一个非零实数，使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行，…，BC为第n行，记点A上的数为a，…第i行中第j个数为a（1≤j≤i）.若a=
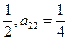
（1）求a
（2）试归纳出第n行中第m个数a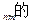表达式（用含n,m的式子表示，不必证明）；
（3）记S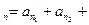…+a，证明：n≤++…+≤
粤公网安备 44130202000953号