设函数f ( x ) =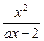 
(a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
f (– m ) < –
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若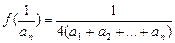
对任意nÎN*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
的值域为
，
的取值范围
解不等式：
的最大值为
，最小值为
，求此函数式
的最大值和最小值；（2）y－x的最小值；（3）x2+y2的最大值和最小值.
y=0，求x+y的最小值.推荐套卷
设函数f ( x ) = 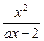(a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
f (– m ) < –成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若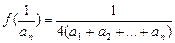对任意nÎN*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
粤公网安备 44130202000953号