设函数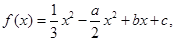 其中
其中 ,曲线
,曲线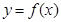 在点
在点 处的切线方程为
处的切线方程为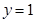 .
.
(I)确定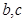 的值;
的值;
(II)设曲线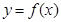 在点
在点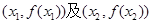 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当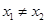 时,
时,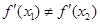 ;
;
(III)若过点(0,2)可作曲线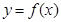 的三条不同切线,求
的三条不同切线,求 的取值范围.
的取值范围.
相关知识点
推荐套卷
设函数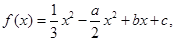 其中
其中 ,曲线
,曲线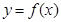 在点
在点 处的切线方程为
处的切线方程为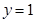 .
.
(I)确定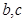 的值;
的值;
(II)设曲线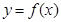 在点
在点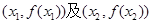 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当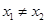 时,
时,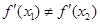 ;
;
(III)若过点(0,2)可作曲线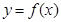 的三条不同切线,求
的三条不同切线,求 的取值范围.
的取值范围.