某公司对营销人员有如下规定：
①年销售额
在9万元以下，没有奖金，
②年销售额（万元），当
时，奖金为
（万元），
且年销售额越大，奖金越多，
③年销售额超过 81万元，按5﹪
发奖金（年销售额万元）.
（1） 求奖金关于的函数解析式；
（2）某营销人员争取年奖金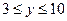
（万元），年销售额在什么范围内？
相关试题
中，角
所对的边分别为
，且满足
，
．（I）求
，求
的值．
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
中，已知
，
．
的值；
，求
的值．
,
，求B.
的最大值.推荐套卷
某公司对营销人员有如下规定：
①年销售额在9万元以下，没有奖金，
②年销售额（万元），当时，奖金为（万元）， 且年销售额越大，奖金越多，
③年销售额超过 81万元，按5﹪发奖金（年销售额万元）.
（1） 求奖金关于的函数解析式；
（2）某营销人员争取年奖金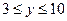（万元），年销售额在什么范围内？
粤公网安备 44130202000953号