已知圆C: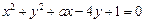
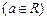，过定点P(0 , 1)作斜率为1的直线交圆C于A、B两点，P为线段AB的中点.
（Ⅰ）求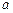
的值；
（Ⅱ）设E为圆C上异于A、B的一点，求△ABE面积的最大值；
（Ⅲ）从圆外一点M向圆C引一条切线，切点为N，且有|MN|="|MP|" , 求|MN|的最小值，并求|MN|取最小值时点M的坐标.
为偶函数，且在区间
上是单调递减函数，
的解析式；
的奇偶性。
，求
的值；
，
，求
的范围.
，且满足
的值；
，
，求
的值。
最大值为
，且
的解析式；
上的最值.
，集合
，
；
；
相关知识点
推荐套卷
已知圆C: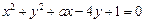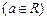，过定点P(0 , 1)作斜率为1的直线交圆C于A、B两点，P为线段AB的中点.
（Ⅰ）求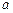的值；
（Ⅱ）设E为圆C上异于A、B的一点，求△ABE面积的最大值；
（Ⅲ）从圆外一点M向圆C引一条切线，切点为N，且有|MN|="|MP|" , 求|MN|的最小值，并求|MN|取最小值时点M的坐标.
粤公网安备 44130202000953号