如图,在梯形ABCD中,AB∥CD,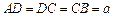 ,
,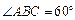 ,平面
,平面 平面
平面 ,四边形
,四边形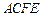 是矩形,
是矩形,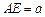 ,点
,点 在线段
在线段 上。
上。
(1)求证: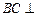 平面
平面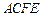 ;
;
(2)当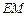 为何值时,
为何值时,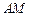 ∥平面
∥平面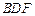 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
推荐套卷
如图,在梯形ABCD中,AB∥CD,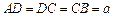 ,
,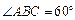 ,平面
,平面 平面
平面 ,四边形
,四边形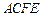 是矩形,
是矩形,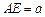 ,点
,点 在线段
在线段 上。
上。
(1)求证: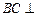 平面
平面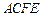 ;
;
(2)当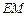 为何值时,
为何值时,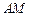 ∥平面
∥平面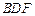 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。