某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别
记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间产品较稳定.
相关知识点
推荐套卷
 ,对任意
,对任意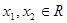 ,恒有
,恒有 ,求:(1)
,求:(1)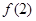 的值;(2)
的值;(2)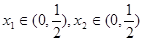 ,都有
,都有 成立时,求
成立时,求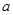 的取值范围.
的取值范围. 表示编号为
表示编号为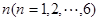 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下: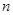
 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差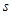 ;
;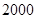 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图:
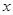 的值;
的值;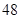 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?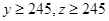 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率. ,
,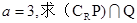 ;(2)若
;(2)若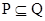 ,求实数
,求实数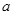 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号