
如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,
AB ="2" , AC = .
.
(I)求证: 平面BCD;
平面BCD;
(II)求二面角A-BC- D的大小;
(III)求O点到平面ACD的距离.
推荐套卷
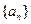 的前
的前 项和为
项和为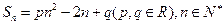
 的值;
的值; ,数列
,数列 }满足
}满足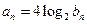 ,求数列
,求数列 的前
的前 中,角
中,角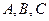 所对的边分别为
所对的边分别为 ,且
,且 .
.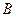 的大小;
的大小;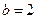 ,
, ,求
,求 .
. ;
; 是(1)中曲线
是(1)中曲线 的取值范围.
的取值范围. ,动点
,动点 到定直线
到定直线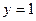 的距离等于
的距离等于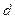 ,并且满足
,并且满足 ,其中
,其中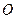 为坐标原点,
为坐标原点,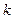 为非负实数.
为非负实数.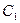 ;
; ,试判断曲线
,试判断曲线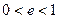 ,当
,当 是曲线
是曲线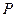 ,使得
,使得 成立,求实数
成立,求实数 的底面为正方形,
的底面为正方形, 底面
底面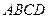 ,
,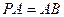 ,
, 为
为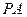 上的点.
上的点.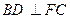 ;
;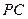 //平面
//平面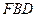 ,求二面角
,求二面角 的余弦值.
的余弦值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号