已知函数f(x)=6x–6x2,设函数g1(x)=f(x), g2(x)=f[g1(x)], g3(x)=f [g2(x)],…gn(x)=f[gn–1(x)],…
(1)求证:如果存在一个实数x0,满足g1(x0)=x0,那么对一切n∈N,gn(x0)=x0都成立;
(2)若实数x0满足gn(x0)=x0,则称x0为稳定不动点,试求出所有这些稳定不动点;
(3)设区间A=(–∞,0),对于任意x∈A,有g1(x)=f(x)=a<0, g2(x)=f[g1(x)]=f(0)<0,
且n≥2时,gn(x)<0 试问是否存在区间B(A∩B≠
试问是否存在区间B(A∩B≠ ),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
推荐套卷
 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为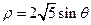 .
.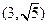 ,求|PA|+|PB|.
,求|PA|+|PB|. 的逆矩阵.
的逆矩阵.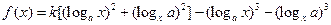 , (其中
, (其中 ),
), ,设
,设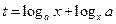 .
. 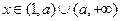 时,试将
时,试将 表示成
表示成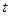 的函数
的函数 ,并探究函数
,并探究函数 ,存在
,存在 ,使
,使 ,试求实数b的取值范围.。
,试求实数b的取值范围.。 ,每生产1件合格产品盈利3元,每出现1件次品亏损1.5元. (I)将日盈利额y(万元)表示为日产量
,每生产1件合格产品盈利3元,每出现1件次品亏损1.5元. (I)将日盈利额y(万元)表示为日产量 (万件)的函数;(Ⅱ)为使日盈利额最大,日产量应为多少万件?
(万件)的函数;(Ⅱ)为使日盈利额最大,日产量应为多少万件? 粤公网安备 44130202000953号
粤公网安备 44130202000953号