设数列{an}的首项a1=1，前n项和Sn满足关系式:3tSn－(2t+3)Sn－1=3t(t＞0,n=2,3,4…).
(1)求证: 数列{an}是等比数列；
(2)设数列{an}的公比为f(t)，作数列{bn}，使b1=1,bn=f(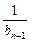
)(n=2,3,4…)，求数列{bn}的通项bn；
(3)求和: b1b2－b2b3+b3b4－…+b2n－1b2n－b2nb2n+1.
相关试题
的底面为直角梯形，
，
底面
，且
，
，
是
的中点。
面
；
与
与面
所成二面角的余弦值。
方程
有两个不等的正实数根，命题
方程
无实数根。若“
或
”为真命题，求
的取值范围。
对任意实数
都有
且
时
。
内是增函数；
，试求
的取值范围。
中，棱长是1，
；
的距离。
的方程是
，点
。
且与推荐套卷
设数列{an}的首项a1=1，前n项和Sn满足关系式:3tSn－(2t+3)Sn－1=3t(t＞0,n=2,3,4…).
(1)求证: 数列{an}是等比数列；
(2)设数列{an}的公比为f(t)，作数列{bn}，使b1=1,bn=f(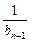)(n=2,3,4…)，求数列{bn}的通项bn；
(3)求和: b1b2－b2b3+b3b4－…+b2n－1b2n－b2nb2n+1.
粤公网安备 44130202000953号