在2008年春运期间,一名大学生要从广州回到郑州老家有两种选择,即坐火车或汽车。已知该大学生先去买火车票的概率是先去买汽车票概率的3倍,汽车票随时都能买到。若先去买火车票,则买到火车票的概率为0.6,买不到火车票,再去买汽车票。
(I)求这名大学生先去买火车票的概率;
(II)若火车票的价格为120元,汽车票的价格为280元,设该大学生购买车票所花费钱数为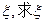 的期望值。
的期望值。
相关知识点
推荐套卷
在2008年春运期间,一名大学生要从广州回到郑州老家有两种选择,即坐火车或汽车。已知该大学生先去买火车票的概率是先去买汽车票概率的3倍,汽车票随时都能买到。若先去买火车票,则买到火车票的概率为0.6,买不到火车票,再去买汽车票。
(I)求这名大学生先去买火车票的概率;
(II)若火车票的价格为120元,汽车票的价格为280元,设该大学生购买车票所花费钱数为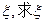 的期望值。
的期望值。