某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并宣
布：观众答对问题A可获奖金2a元；答对问题B可获奖金3a元，答对两题则可获5a元.先答哪个问题由观众选择，只有第1题答对才能答第2题，否则中止答题.若你被选为幸运观众，且假设你答对A、B的概率分别为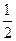
、
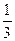，你觉得应先回答哪个问题？说明理由.
相关试题
,解关于x的不等式
.
}是公差不为零的等差数列，
=" 1" ，且
，
成等比数列.
}的前n项和
.
a + b ;
)(1+ 
) ≥ 9 .
,垂足为E,且E是OB的中点，求BC的长。
中，D是AC的中点，E是线段D
O上一点，且
，求异面直线DE与CD
面CD
的值
相关知识点
推荐套卷
某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题，并宣
布：观众答对问题A可获奖金2a元；答对问题B可获奖金3a元，答对两题则可获5a元.先答哪个问题由观众选择，只有第1题答对才能答第2题，否则中止答题.若你被选为幸运观众，且假设你答对A、B的概率分别为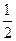、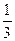，你觉得应先回答哪个问题？说明理由.
粤公网安备 44130202000953号