已知a1=2，点（an，an+1）在函数f(x)=x2+2x的图象上，其中n=1,2,3,…
（1）证明：数列{lg(1+an) }是等比数列.
（2）设Tn=(1+a1)(1+a2)…(1+an)，求Tn及数列{an}的通项.
（3）记bn=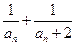
，数列{bn}的前n项和为Sn，求
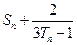的值
的最大值与最小值．推荐套卷
已知a1=2，点（an，an+1）在函数f(x)=x2+2x的图象上，其中n=1,2,3,…
（1）证明：数列{lg(1+an) }是等比数列.
（2）设Tn=(1+a1)(1+a2)…(1+an)，求Tn及数列{an}的通项.
（3）记bn=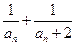，数列{bn}的前n项和为Sn，求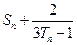的值
粤公网安备 44130202000953号