某港口的水深 (米)是时间
(米)是时间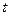 (0≤
(0≤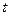 ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数 的图像.
的图像.
(1)试根据以上数据,求出 的表达式;
的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间?(忽略进出港所用的时间)?
推荐套卷
某港口的水深 (米)是时间
(米)是时间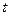 (0≤
(0≤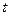 ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数 的图像.
的图像.
(1)试根据以上数据,求出 的表达式;
的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间?(忽略进出港所用的时间)?