(本小题满分12分)设有同频率的两个正弦电流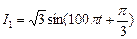 ,
,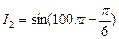 ,把它们合成后,得到电流
,把它们合成后,得到电流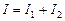 .(1)求电流
.(1)求电流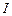 的最小正周期
的最小正周期 和频率
和频率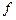 ;(2)设
;(2)设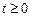 ,求电流
,求电流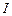 的最大值和最小值,并指出
的最大值和最小值,并指出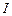 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的 值.
值.
相关知识点
推荐套卷
(本小题满分12分)设有同频率的两个正弦电流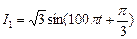 ,
,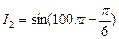 ,把它们合成后,得到电流
,把它们合成后,得到电流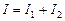 .(1)求电流
.(1)求电流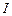 的最小正周期
的最小正周期 和频率
和频率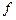 ;(2)设
;(2)设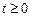 ,求电流
,求电流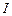 的最大值和最小值,并指出
的最大值和最小值,并指出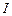 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的 值.
值.