用一枚质地均匀的硬币,甲、乙两人做抛掷硬币游戏,甲抛掷4次,记正面朝上的次为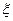 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为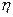 .(Ⅰ)分别求
.(Ⅰ)分别求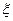 和
和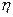 的期望;(Ⅱ)规定:若
的期望;(Ⅱ)规定:若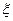 >
>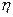 ,则甲获胜;否则,乙获胜.求甲获胜的概率.
,则甲获胜;否则,乙获胜.求甲获胜的概率.
相关知识点
推荐套卷
用一枚质地均匀的硬币,甲、乙两人做抛掷硬币游戏,甲抛掷4次,记正面朝上的次为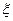 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为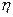 .(Ⅰ)分别求
.(Ⅰ)分别求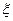 和
和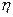 的期望;(Ⅱ)规定:若
的期望;(Ⅱ)规定:若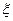 >
>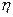 ,则甲获胜;否则,乙获胜.求甲获胜的概率.
,则甲获胜;否则,乙获胜.求甲获胜的概率.