在平面直角坐标系中,已知A1(-3,0),A2(3,0),P(x,y),M( ,0),若实数λ使向量
,0),若实数λ使向量 ,λ
,λ ,
,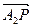 满足λ2·(
满足λ2·( )2=
)2= ·
·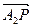 。
。
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当λ=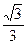 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
推荐套卷
在平面直角坐标系中,已知A1(-3,0),A2(3,0),P(x,y),M( ,0),若实数λ使向量
,0),若实数λ使向量 ,λ
,λ ,
,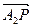 满足λ2·(
满足λ2·( )2=
)2= ·
·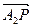 。
。
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当λ=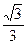 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。