三个元件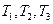
正常工作的概率分别为
将它们中某两个元件并联后再和第三元件串联接入电路.
（Ⅰ）在如图的电路中，电路不发生故障的概率是多少？
|
（Ⅱ）三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.
，
,
的单调性，并证明；
和
的值
时，求
的值
.
的值；（2）计算：
.
，
；（2）求
；
的定义域； 相关知识点
推荐套卷
三个元件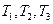正常工作的概率分别为将它们中某两个元件并联后再和第三元件串联接入电路.
（Ⅰ）在如图的电路中，电路不发生故障的概率是多少？
|
（Ⅱ）三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.
粤公网安备 44130202000953号