已知f(x)在(－1，1)上有定义，f(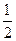
)＝－1，且满足x，y∈(－1，1)有f(x)＋f(y)＝f(
)
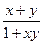⑴证明：f(x)在(－1，1)上为奇函数；
⑵对数列x1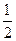＝，xn＋1＝
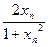，求f(xn);
⑶求证
是等差数列，其中
，（1）求
值．
均为正数，证明：
，
，且
,求证：
.相关知识点
推荐套卷
已知f(x)在(－1，1)上有定义，f(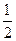)＝－1，且满足x，y∈(－1，1)有f(x)＋f(y)＝f()
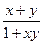⑴证明：f(x)在(－1，1)上为奇函数；
⑵对数列x1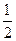＝，xn＋1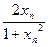＝，求f(xn);
⑶求证
粤公网安备 44130202000953号