（本小题满分13分）已知函数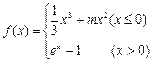
（1）讨论函数f (x)的极值情况； （2）设g (x) = ln(x + 1)，当x1>x2>0时，试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小；并说明理由．
推荐套卷
（本小题满分13分）已知函数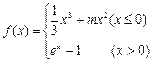 （1）讨论函数f (x)的极值情况； （2）设g (x) = ln(x + 1)，当x1>x2>0时，试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小；并说明理由．
粤公网安备 44130202000953号