(本小题满分12分)
如图，函数f1（x）＝A sin（wx＋j）（A＞0，w＞0，｜j｜＜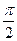
）的一段图象，过点（0，1）．（1）求函数f1（x）的解析式；（2）将函数y＝f1（x）的图象按向量
＝
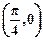平移，得到函数y＝f2（x），求y＝f1（x）＋f2（x）的最大值，并求此时自变量x的集合．
是奇函数，
的值；
，求
的值.
求集合
.
，定义面积函数
为直线
与
的值为（）
和
是函数
的两个极值点，其中
.
的取值范围；
，求
的最大值（注:
是自然对数的底数）.
上函数
对任意正数
都有
，当
时，
，且
.
的值；
的不等式
.相关知识点
推荐套卷
(本小题满分12分)
如图，函数f1（x）＝A sin（wx＋j）（A＞0，w＞0，｜j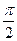｜＜）的一段图象，过点（0，1）．（1）求函数f1（x）的解析式；（2）将函数y＝f1（x）的图象按向量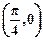＝平移，得到函数y＝f2（x），求y＝f1（x）＋f2（x）的最大值，并求此时自变量x的集合．
粤公网安备 44130202000953号