(本小题满分12分)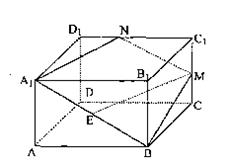
如图，在正四棱柱ABCD—A1B1C1D1中，AA1=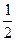
AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.
（Ⅰ）求证：EM∥平面A1B1C1D1；
（Ⅱ）求二面角B—A1N—B1的正切值.
相关试题
在
处取得极值
，其中
为常数.
的值；
的单调区间；
，不等式
恒成立，求c的取值范围.
，其中
.
时，求曲线
在点
处的切线方程；
的单调性.
，且
，求证：
.
，
，其中
．设两曲线
，
有公共点，且在该点处的切线相同．
表示
，并求
时，
的大小，并证明．
，求推荐套卷
(本小题满分12分)
如图，在正四棱柱ABCD—A1B1C1D1中，AA1=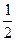AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.
（Ⅰ）求证：EM∥平面A1B1C1D1；
（Ⅱ）求二面角B—A1N—B1的正切值.
粤公网安备 44130202000953号