湖北省荆门市高一下学期期末质量检测数学试卷
设 表示两条直线,
表示两条直线, 表示两个平面,则下列结论正确的是
表示两个平面,则下列结论正确的是
A.若 ∥ ∥ 则 则 ∥ ∥ |
B.若 ∥ ∥ 则 则 ∥ ∥ |
C.若 ∥ ∥ , , 则 则 |
D.若 ∥ ∥ , , 则 则 |
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f(1) = -2 |
f(1.5) = 0.625 |
f(1.25) = -0.984 |
| f(1.375) = -0.260 |
f(1.4375) = 0.162 |
f(1.40625) = -0.054 |
那么方程 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为
A.1.2 B.1.3 C.1.4 D.1.5
《莱因德纸草书》(Rh1nd Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把 个面包分给
个面包分给 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小
是较小的两份之和,则最小 份为
份为
A. |
B. |
C. |
D. |
襄荆高速公路连接襄阳、荆门、荆州三市,全长约188公里,是湖北省大三角经济主骨架的干线公路之一.若某汽车从进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶,已知该汽车每小时的运输成本由固定部分和可变部分组成,固定部分为200元,可变部分与速度v(千米/时)的平方成正比(比例系数记为k).当汽车以最快速度行驶时,每小时的运输成本为488元.若使汽车的全程运输成本最低,其速度为
| A.80 km /小时 | B.90 km /小时 | C.100 km /小时 | D.110 km /小时 |
如图,一个质点从原点出发,在与x轴、y轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,1)→(2,2)→(1,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2014秒时,这个质点所处位置的坐标是
A. |
B. |
C. |
D. |
如图,某海事部门举行安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为 千米/分钟.(用含根号的式子表示)
设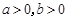 ,则
,则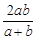 为
为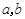 的调和平均数.如图,
的调和平均数.如图,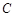 为线段
为线段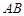 上的点,
上的点,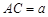 ,
, ,
,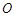 为
为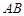 的中点,以
的中点,以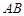 为直径作半圆.过点
为直径作半圆.过点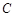 作
作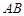 的垂线交半圆于
的垂线交半圆于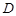 ,连结
,连结 .过点
.过点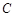 作
作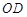 的垂线,垂足为
的垂线,垂足为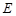 .则图中线段
.则图中线段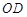 的长度为
的长度为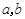 的算术平均数,线段 的长度是
的算术平均数,线段 的长度是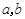 的几何平均数,线段 的长度是
的几何平均数,线段 的长度是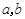 的调和平均数.
的调和平均数.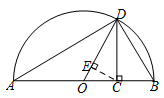
如图,在直三棱柱 中,
中, ,且
,且 .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)若 分别为是
分别为是 和
和 的中点,求证:
的中点,求证: ‖平面
‖平面 .
.
已知△ 的三个内角
的三个内角 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量 ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,判断△
,判断△ 的形状.
的形状.
某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往 地至少72吨的货物,派用的每辆车须满载且只运送一次.派用的每吨甲型卡车须配2名工人,运送一次可得利润450元;派用的每辆乙型卡车须配1名工人,运送一次可得利润350元.问该公司如何派用两类卡车的车辆数可得最大利润?
地至少72吨的货物,派用的每辆车须满载且只运送一次.派用的每吨甲型卡车须配2名工人,运送一次可得利润450元;派用的每辆乙型卡车须配1名工人,运送一次可得利润350元.问该公司如何派用两类卡车的车辆数可得最大利润?
设公差不为0的等差数列 的首项为1,且
的首项为1,且 构成等比数列.
构成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 …
… 1-
1- ,n∈N*,求
,n∈N*,求 的前n项和
的前n项和 .
.
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积 的大小;
的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A-ED-B的正弦值.
 ,集合
,集合 ,则
,则




 为第二象限的角,则下列各式恒小于零的是
为第二象限的角,则下列各式恒小于零的是



 的图象向左平移
的图象向左平移 个单位,所得图象的函数解析式是
个单位,所得图象的函数解析式是



 中,
中, 为△
为△ 等于
等于







 的图象经过点
的图象经过点 , 则
, 则 的值是 .
的值是 . ,
, ,
, ,若
,若 ,
, ∥
∥ ,则
,则 的夹角为 .
的夹角为 . ,各项为正数的等比数列
,各项为正数的等比数列 中,
中, ,则
,则 …
… .
. 、
、 是函数
是函数 图象上任意两点,且
图象上任意两点,且 .
. 的值;
的值; …
… (其中
(其中 ),求
),求 ;
; (
( …
… 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号