全国普通高等学校招生统一考试文科数学
设、是实数,则""是""的()
| A. | 充分而不必要条件 | B. | 必要而不必要条件 |
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
来源:2014年全国普通高等学校招生统一考试文科数学
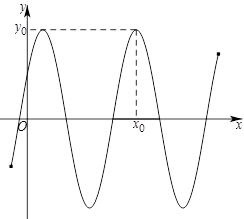
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为"可食用率".在特定条件下,可食用率与加工时间(单位:分钟)满足的函数关系是常数),下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )
| A. | 3.50分钟 | B. | 3.75分钟 | C. | 4.00分钟 | D. | 4.25分钟 |
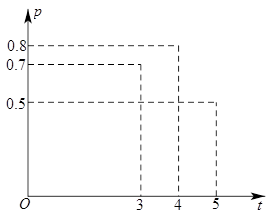
来源:2014年全国普通高等学校招生统一考试文科数学
顾客请一位工艺师把、两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都
完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
| 工序 时间 原料 |
粗加工 |
精加工 |
| 原料 | 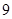 |
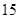 |
| 原料 | 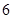 |
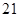 |
则最短交货期为工作日.
来源:2014年全国普通高等学校招生统一考试文科数学
已知
是等差数列,满足
,数列
满足
,且
是等比数列.
(1)求数列
和
的通项公式;
(2)求数列
的前
项和.
来源:2014年全国普通高等学校招生统一考试文科数学
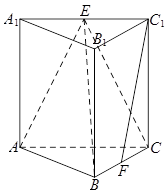
如图,在三棱柱中,侧棱垂直于底面,,,、分别为、的中点.
(1)求证:平面平面;
(2)求证:平面;
(3)求三棱锥的体积.
来源:2014年全国普通高等学校招生统一考试文科数学
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
来源:2014年全国普通高等学校招生统一考试文科数学
 粤公网安备 44130202000953号
粤公网安备 44130202000953号