从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：
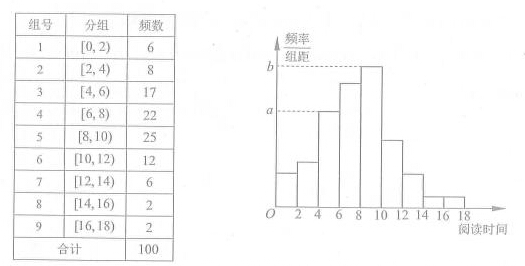
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
（2）求频率分布直方图中的的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）
相关试题
，求此抛物线的方程
上
，右顶点为
.
与双曲线恒有两个不同的交点A和B且
（其中
为原点），求k的取值范围
的两个焦点为
，点P是双曲线C上的一点，
，且
．
；
两点，若
，
，求双曲线C的方程．相关知识点
推荐套卷
从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
（2）求频率分布直方图中的的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）
粤公网安备 44130202000953号