全国普通高等学校招生统一考试理科数学
某地区空气质量监测资料表明,一天的空气质量为优良的概率是,连续两天为优良的概率是,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是()
| A. | B. | C. | D. |
来源:2014年全国普通高等学校招生统一考试理科数学
如图,网格纸上正方形小格的边长为1(表示1),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3,高为6的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()
| A. | B. | C. | D. |
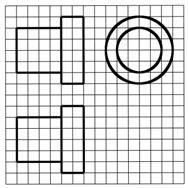
来源:2014年全国普通高等学校招生统一考试理科数学
某地区2007年至2013年农村居民家庭纯收入(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| 年份代号 | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入 | 2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(1)求关于的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
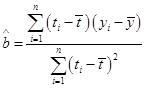 ,
,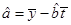
来源:2014年全国普通高等学校招生统一考试理科数学
设分别是椭圆的左右焦点,是上一点且与轴垂直,直线与的另一个交点为.
(1)若直线的斜率为,求的离心率;
(2)若直线在轴上的截距为2,且,求.
来源:2014年全国普通高等学校招生统一考试理科数学
已知函数
.
(1)讨论
的单调性;
(2)设
,当
时,
,求
的最大值;
(3)已知
,估计
的近似值(精确到0.001).
来源:2014年全国普通高等学校招生统一考试理科数学
在直角坐标系中,以坐标原点为极点,轴为极轴建立极坐标系,半圆的极坐标方程为,.
(1)求的参数方程;
(2)设点在上,在处的切线与直线垂直,根据(1)中你得到的参数方程,确定的坐标.
来源:2014年全国普通高等学校招生统一考试理科数学
 粤公网安备 44130202000953号
粤公网安备 44130202000953号