广东省广州市普通高中毕业班综合测试二理科数学试卷
命题“对任意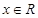 ,都有
,都有 ”的否定是( )
”的否定是( )
A.存在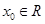 ,使得 ,使得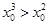 |
B.不存在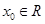 ,使得 ,使得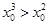 |
C.存在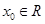 ,使得 ,使得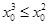 |
D.对任意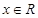 ,都有 ,都有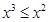 |
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
将函数 的图象向左平移
的图象向左平移 个单位长度后得到函数
个单位长度后得到函数 ,则函数
,则函数 ( )
( )
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数,也不是偶函数 |
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
有两张卡片,一张的正反面分别写着数字 与
与 ,另一张的正反面分别写着数字
,另一张的正反面分别写着数字 与
与 ,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
A. |
B. |
C. |
D. |
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
设 、
、 分别是椭圆
分别是椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆
在椭圆 上,线段
上,线段 的中点在
的中点在 轴上,若
轴上,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A. |
B. |
C. |
D. |
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
将正偶数 、
、 、
、 、
、 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记 表示第
表示第 行和第
行和第 列的数,若
列的数,若 ,则
,则 的值为( )
的值为( )
| |
第 列 列 |
第 列 列 |
第 列 列 |
第 列 列 |
第 列 列 |
第 行 行 |
|
 |
 |
 |
 |
第 行 行 |
 |
 |
 |
 |
|
第 行 行 |
|
 |
 |
 |
 |
第 行 行 |
 |
 |
 |
 |
|
第 行 行 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
A. B.
B. C.
C. D.
D.
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图
(1)求 的值;
的值;
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第 组的频率为
组的频率为 ,第
,第 组区间的中点值为
组区间的中点值为 ,则样本数据的平均值为
,则样本数据的平均值为 .)
.)
(3)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
如图,在五面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
已知数列 的前
的前 项和为
项和为 ,且
,且 ,对任意
,对任意 ,都有
,都有
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
已知定点 和直线
和直线 ,过点
,过点 且与直线
且与直线 相切的动圆圆心为点
相切的动圆圆心为点 ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)若点 的坐标为
的坐标为 ,直线
,直线 (
( ,且
,且 )与抛物线
)与抛物线 ,相交于
,相交于 、
、 两点,直线
两点,直线 、
、 分别交直线
分别交直线 于点
于点 、
、 试判断以线段
试判断以线段 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
来源:2014届广东省广州市普通高中毕业班综合测试二理科数学试卷
 满足
满足 ,其中
,其中 为虚数单位,则
为虚数单位,则



 是函数
是函数 的反函数,则
的反函数,则 的值为( )
的值为( )








 的解集为.
的解集为. 的展开式的常数项是第
的展开式的常数项是第 项,则正整数
项,则正整数 的值为.
的值为. 是边长为
是边长为 的正方形,若
的正方形,若 ,
, ,则
,则 的值为.
的值为. 的正方形,若
的正方形,若 、
、 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为
的最大值为 ,则
,则 的最大值为.
的最大值为. 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, .设函数
.设函数 ,当
,当 时,函数
时,函数 的值域为集合
的值域为集合 ,则
,则 中,直线
中,直线 (
( 为参数)与圆
为参数)与圆 (
( 为参数)相切,切点在第一象限,则实数
为参数)相切,切点在第一象限,则实数 的值为.
的值为. 中,点
中,点 在线段
在线段 上,且
上,且 ,连接
,连接 ,若
,若 与
与 ,
, 的面积为
的面积为 ,则
,则 的面积为
的面积为 .
. 中,
中, 是边
是边 的中点,且
的中点,且 ,
, .
.
 的值;
的值; 的值.
的值. 在点
在点 处的切线方程为
处的切线方程为
 .
. 、
、 的值;
的值; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且
,且 时,
时, .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号