一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取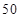
个作为样本，称出它们的重量（单位：克），重量分组区间为
，
，
，
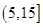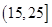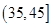，由此得到样本的重量频率分布直方图，如图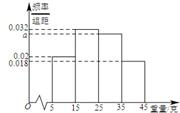
（1）求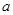
的值；
（2）根据样本数据，试估计盒子中小球重量的平均值；
（注：设样本数据第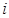
组的频率为
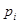，第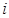组区间的中点值为
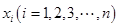，则样本数据的平均值为
.）
（3）从盒子中随机抽取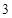
个小球，其中重量在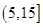内的小球个数为
，求的分布列和数学期望.
，点
，在第一象限的动点
满足
，求点
，若方程
有两个实数解，求实数
的取值范围．
的两个定圆的切线长相等的点的轨迹是直线．
点射出，到
轴上的
点后被
轴上的
点，又被
，求
所在直线的方程．
满足什么条件时，
：
，
：
，
：
三条直线只有两个交点？推荐套卷
一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取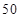个作为样本，称出它们的重量（单位：克），重量分组区间为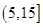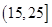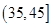，，，，由此得到样本的重量频率分布直方图，如图
（1）求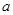的值；
（2）根据样本数据，试估计盒子中小球重量的平均值；
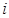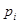（注：设样本数据第组的频率为，第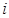组区间的中点值为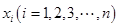，则样本数据的平均值为.）
（3）从盒子中随机抽取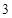个小球，其中重量在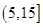内的小球个数为，求的分布列和数学期望.
粤公网安备 44130202000953号