2007年全国统一高考理科数学试卷(上海卷)
若
为非零实数,则下列四个命题都成立:
①
②
③若
,则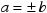 ④若
,则
④若
,则
则对于任意非零复数 ,上述命题仍然成立的序号是。
平面内两直线有三种位置关系:相交,平行与重合.已知两个相交平面 与两直线 ,又知 在 内的射影为 ,在 内的射影为 .试写出 与 满足的条件,使之一定能成为 是异面直线的充分条件.
已知圆的方程 , 为圆上任意一点(不包括原点)。直线 的倾斜角为 弧度, ,则 的图象大致为 .
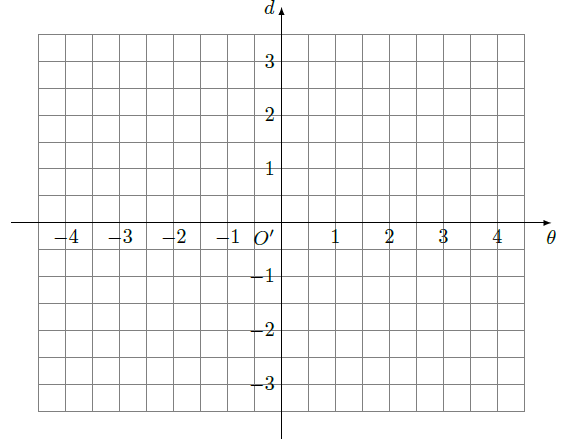
在直角坐标系 中, 分别是与 轴, 轴平行的单位向量,若直角三角形 中, , ,则 的可能值有
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
已知 是定义域为正整数集的函数,对于定义域内任意的 ,若 成立,则 成立,下列命题成立的是()
| A. | 若 成立,则对于任意 ,均有 成立; |
| B. | 若 成立,则对于任意的 ,均有 成立; |
| C. | 若 成立,则对于任意的 ,均有 成立; |
| D. | 若 成立,则对于任意的 ,均有 成立。 |
近年来,太阳能技术运用的步伐日益加快,已知
年全球太阳能年生产量为
兆瓦,年增长率为
。在此后的四年里,增长率以每年
的速度增长(例如2003年的年生产量增长率为
)
(1)求
年的太阳能年生产量(精确到
兆瓦)
(2)已知
年太阳能年安装量为
兆瓦,在此后的
年里年生产量保持
的增长率,若
年的年安装量不少于年生产量的
,求
年内年安装量的增长率的最小值(精确到
)
若有穷数列
(
是正整数),满足
即
(
是正整数,且
),就称该数列为"对称数列"。
(1)已知数列
是项数为7的对称数列,且
成等差数列,
,试写出
的每一项
(2)已知
是项数为
的对称数列,且
构成首项为50,公差为
的等差数列,数列
的前
项和为
,则当
为何值时,
取到最大值?最大值为多少?
(3)对于给定的正整数
,试写出所有项数不超过
的对称数列,使得
成为数列中的连续项;当
时,试求其中一个数列的前2008项和
 粤公网安备 44130202000953号
粤公网安备 44130202000953号