2013年全国统一高考理科数学试卷(四川卷)
从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为 ,共可得到 的不同值的个数是()
| A. | 9 | B. | 10 | C. | 18 | D. | 20 |
节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
| A. | B. | C. | D. |
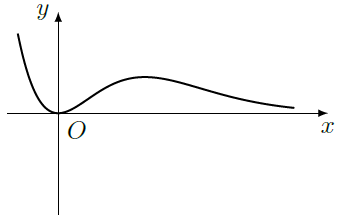
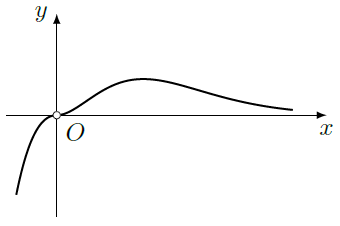
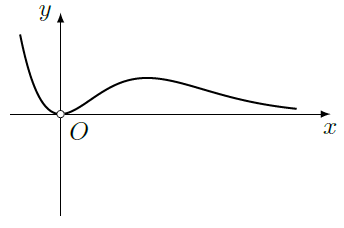
设函数 ( , 为自然对数的底数),若曲线 上存在点 使得 ,则 的取值范围是()
| A. | [ ] | B. | [ ] | C. | [ ] | D. | [ ] |
设 为平面 内的 个点,在平面 内的所有点中,若点 到点 的距离之和最小,则称点 为 的一个"中位点",例如,线段 上的任意点都是端点 的中位点,现有下列命题:
①若三个点 共线, 在线段 上,则 是 的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点
共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是(写出所有真命题的序号).
某算法的程序框图如图所示,其中输入的变量 在1,2,3,…,24这24个整数中等可能随机产生

(I)分别求出按程序框图正确编程运行时输出
的值为
的概率
;
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行
次后,统计记录输出y的值为
的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数 | 输出
的值为1的频数 |
输出
的值为2的频数 |
输出
的值为3的频数 |
| 30 |
14 |
6 |
10 |
| … |
… |
… |
… |
| 2100 |
1027 |
376 |
697 |
乙的频数统计图(部分)
| 运行次数 | 输出
的值为1的频数 |
输出y的值为2的频数 |
输出
的值为3的频数 |
| 30 |
12 |
11 |
7 |
| … |
… |
… |
… |
| 2100 |
1051 |
696 |
353 |
当
时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为
的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出
的值为2的次数
的分布列及数学期望.
如图,在三棱柱
中,侧棱
底面
,
,
120°,
分别是线段
的中点,
是线段
的中点.

(I)在平面
内,试做出过点
与平面
平行的直线
,说明理由,并证明直线
平面
;
(II)设(I)中的直线
交
于点
,交
于点
,求二面角
的余弦值.
已知椭圆
(
)的两个焦点分别为
,
,且椭圆
经过点
.
(I)求椭圆
的离心率:
(II)设过点
的直线
与椭圆
交于
两点,点
是线段
上的点,且
,求点
的轨迹方程.







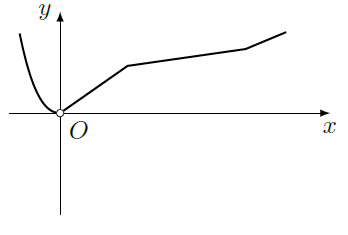
 粤公网安备 44130202000953号
粤公网安备 44130202000953号