如图,在三棱柱
中,侧棱
底面
,
,
120°,
分别是线段
的中点,
是线段
的中点.
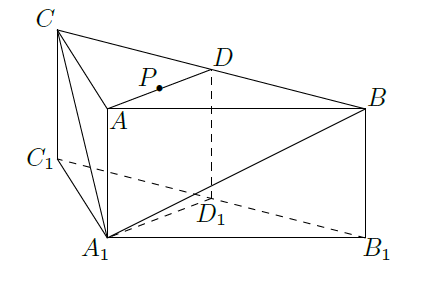
(I)在平面
内,试做出过点
与平面
平行的直线
,说明理由,并证明直线
平面
;
(II)设(I)中的直线
交
于点
,交
于点
,求二面角
的余弦值.
推荐套卷
如图,在三棱柱
中,侧棱
底面
,
,
120°,
分别是线段
的中点,
是线段
的中点.

(I)在平面
内,试做出过点
与平面
平行的直线
,说明理由,并证明直线
平面
;
(II)设(I)中的直线
交
于点
,交
于点
,求二面角
的余弦值.