为了解某市的交通状况，现对其6条道路进行评估，得分分别为：5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表：
| 评估的平均得分 |
 |
 |
 |
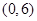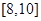| 全市的总体交通状况等级 |
不合格 |
合格 |
优秀 |
（1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级；
（2）用简单随机抽样方法从这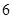
条道路中抽取
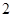条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过
的概率.
，求c边的长。
若
,且
成等比数列，求
中，内角
、
、
所对的边分别是
、
、
，已知
，
，
，求
，△
，试求函数
的最大值.推荐套卷
为了解某市的交通状况，现对其6条道路进行评估，得分分别为：5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表：
| 评估的平均得分 |
|
|
|
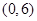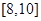| 全市的总体交通状况等级 |
不合格 |
合格 |
优秀 |
（1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级；
（2）用简单随机抽样方法从这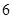条道路中抽取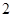条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过的概率.
粤公网安备 44130202000953号